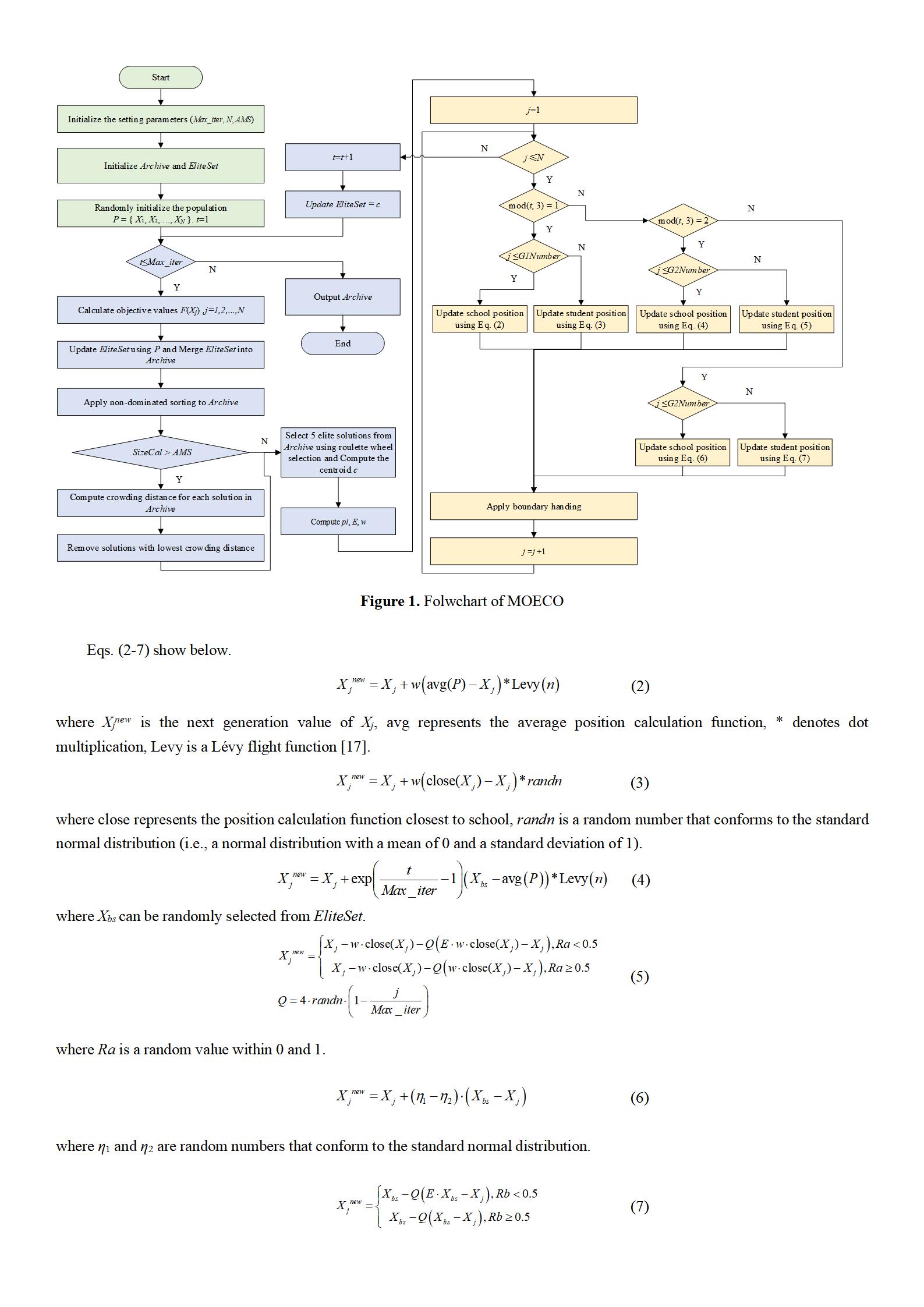
Educational Competition Optimization (ECO), as a new metaheuristic algorithm, performs well in single-objective optimization problems, but it is difficult to apply to multi-objective complex optimization problems. Hence, a Multi-Objective Educational Competition Optimization (MOECO) based on the Pareto improvement and the roulette strategy is proposed. In order to verify the effect of MOECO in engineering application, MOECO was used to solve the hobbing control parameter optimization model. Compared with the Multi-Objective Gray Wolf Algorithm (MOGWO) and the Multi-Objective Runge Kutta Optimizer (MORUN), the experimental results show that MOECO is feasible and effective in this engineering case. MOECO provides a new solution for complex multi-objective optimization problems, which has theoretical value and engineering application potential.






Hakim, W.L.; Fadhillah, M.F.; Won, J.-S.; Park, Y.-C.; Lee, C.-W. Advanced time-series InSAR analysis to estimate surface deformation and utilization of hybrid deep learning for susceptibility mapping in the Jakarta metropolitan region. GISci. Remote Sens. 2025, 62(1), 2465349.
Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69(3), 46–61.
Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872.
Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2022, 30(1), 427–455.
Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56(12), 15217–15270.
Dhiman, G.; Kumar, V. Multi-objective spotted hyena optimizer: A Multi-objective optimization algorithm for engineering problems. Knowl.-Based Syst. 2018, 150, 175–197.
El-rayes, K.; Kandil, A. Time-Cost-Quality Trade-Off Analysis for Highway Construction. J. Constr. Eng. Manag. 2005, 131(4), 477–486.
Ozcan-Deniz, G.; Zhu, Y.; Ceron, V. Time, Cost, and Environmental Impact Analysis on Construction Operation Optimization Using Genetic Algorithms. J. Manag. Eng. 2012, 28(3), 265–272.
Parente, M.; Cortez, P.; Gomes Correia, A. An evolutionary multi-objective optimization system for earthworks. Expert Syst. Appl. 2015, 42(19), 6674–6685.
Ozcan-Deniz, G.; Zhu, Y. Multi-objective optimization of greenhouse gas emissions in highway construction projects. Sustain. Cities Soc. 2017, 28, 162–171.
Liu, L.; Zhang, C. Research on multi-objective optimization of construction engineering based on improved genetic algorithm. Procedia Comput. Sci. 2023, 228, 1086–1091.
Zhang, H.; Xing, F. Fuzzy-multi-objective particle swarm optimization for time–cost–quality tradeoff in construction. Autom. Constr. 2010, 19(8), 1067–1075.
Liu, S.; Tao, R.; Tam, C.M. Optimizing cost and CO2 emission for construction projects using particle swarm optimization. Habitat Int. 2013, 37, 155–162.
Dhiman, G.; Kumar, V. Multi-objective spotted hyena optimizer: A Multi-objective optimization algorithm for engineering problems. Knowl.-Based Syst. 2018, 150, 175–197.
Das, A.K.; Pratihar, D.K. A novel approach for neuro-fuzzy system-based multi-objective optimization to capture inherent fuzziness in engineering processes. Knowl.-Based Syst. 2019, 175, 1–11.
Zouache, D.; Abdelaziz, F.B. Guided Manta Ray foraging optimization using epsilon dominance for multi-objective optimization in engineering design. Expert Syst. Appl. 2022, 189, 116126.
Lian, J.; Zhu, T.; Ma, L.; Wu, X.; Heidari, A.A.; Chen, Y.; Chen, H.; Hui, G. The educational competition optimizer. Int. J. Syst. Sci. 2024, 55(15), 3185–3222.
Cao, W.; Yu, Y.; Li, J.; Wu, D.; Ni, J.; Chen, X. High stability multi-objective decision-making approach of dry hobbing parameters. J. Manuf. Process. 2022, 84, 1184–1195.
Cao, W.; Chen, X.; Ni, J. Fuzzy decision-making approach of hobbing tool and cutting parameters. Eng. Appl. Artif. Intell. 2023, 125, 106655.
Cao, W.; Ni, J.; Jiang, B.; Ye, C. A three-stage parameter prediction approach for low-carbon gear hobbing. J. Clean. Prod. 2021, 289, 125777.
Chen, X.; Li, X.; Li, Z. Control parameter optimization of dry hobbing under user evaluation. J. Manuf. Process. 2025, 133, 46–54.
Ni, H.; Yan, C.; Ni, S.; Shu, H.; Zhang, Y. Multi-verse optimizer based parameters decision with considering tool life in dry hobbing process. Adv. Manuf. 2021, 9(2), 216–234.